Understanding how LLM inference works with llama.cpp

In this post, we will dive into the internals of Large Language Models (LLMs) to gain a practical understanding of how they work. To aid us in this exploration, we will be using the source code of llama.cpp, a pure c++ implementation of Meta’s LLaMA model. Personally, I have found llama.cpp to be an excellent learning aid for understanding LLMs on a deeper level. Its code is clean, concise and straightforward, without involving excessive abstractions. We will use this commit version.

We will focus on the inference aspect of LLMs, meaning: how the already-trained model generates responses based on user prompts.

This post is written for engineers in fields other than ML and AI who are interested in better understanding LLMs. It focuses on the internals of an LLM from an engineering perspective, rather than an AI perspective. Therefore, it does not assume extensive knowledge in math or deep learning.

Throughout this post, we will go over the inference process from beginning to end, covering the following subjects (click to jump to the relevant section):

• Tensors: A basic overview of how the mathematical operations are carried out using tensors, potentially offloaded to a GPU.
• Tokenization: The process of splitting the user’s prompt into a list of tokens, which the LLM uses as its input.
• Embedding: The process of converting the tokens into a vector representation.
• The Transformer: The central part of the LLM architecture, responsible for the actual inference process. We will focus on the self-attention mechanism.
• Sampling: The process of choosing the next predicted token. We will explore two sampling techniques.
• The KV cache: A common optimization technique used to speed up inference in large prompts. We will explore a basic kv cache implementation.

By the end of this post you will hopefully gain an end-to-end understanding of how LLMs work. This will enable you to explore more advanced topics, some of which are detailed in the last section.

Table of contents

High-level flow from prompt to output

As a large language model, LLaMA works by taking an input text, the “prompt”, and predicting what the next tokens, or words, should be.

To illustrate this, we will use the first sentence from the Wikipedia article about Quantum Mechanics as an example. Our prompt is:

Quantum mechanics is a fundamental theory in physics that

The LLM attempts to continue the sentence according to what it was trained to believe is the most likely continuation. Using llama.cpp, we get the following continuation:

provides insights into how matter and energy behave at the atomic scale.

Let’s begin by examining the high-level flow of how this process works. At its core, an LLM only predicts a single token each time. The generation of a complete sentence (or more) is achieved by repeatedly applying the LLM model to the same prompt, with the previous output tokens appended to the prompt. This type of model is referred to as an autoregressive model. Thus, our focus will primarily be on the generation of a single token, as depicted in the high-level diagram below:

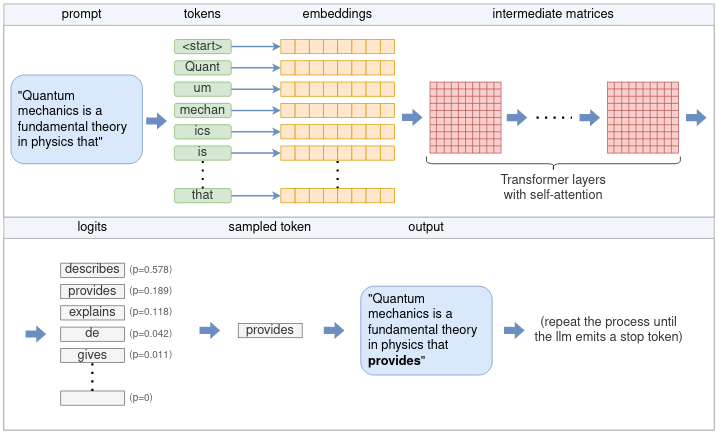
Following the diagram, the flow is as follows:

1. The tokenizer splits the prompt into a list of tokens. Some words may be split into multiple tokens, based on the model’s vocabulary. Each token is represented by a unique number.
2. Each numerical token is converted into an embedding. An embedding is a vector of fixed size that represents the token in a way that is more efficient for the LLM to process. All the embeddings together form an embedding matrix.
3. The embedding matrix serves as the input to the Transformer. The Transformer is a neural network that acts as the core of the LLM. The Transformer consists of a chain of multiple layers. Each layer takes an input matrix and performs various mathematical operations on it using the model parameters, the most notable being the self-attention mechanism. The layer’s output is used as the next layer’s input.
4. A final neural network converts the output of the Transformer into logits. Each possible next token has a corresponding logit, which represents the probability that the token is the “correct” continuation of the sentence.
5. One of several sampling techniques is used to choose the next token from the list of logits.
6. The chosen token is returned as the output. To continue generating tokens, the chosen token is appended to the list of tokens from step (1), and the process is repeated. This can be continued until the desired number of tokens is generated, or the LLM emits a special end-of-stream (EOS) token.

In the following sections, we will delve into each of these steps in detail. But before doing that, we need to familiarize ourselves with tensors.

Understanding tensors with ggml

Tensors are the main data structure used for performing mathemetical operations in neural networks. llama.cpp uses ggml, a pure C++ implementation of tensors, equivalent to PyTorch or Tensorflow in the Python ecosystem. We will use ggml to get an understanding of how tensors operate.

A tensor represents a multi-dimensional array of numbers. A tensor may hold a single number, a vector (one-dimensional array), a matrix (two-dimensional array) or even three or four dimensional arrays. More than is not needed in practice.

It is important to distinguish between two types of tensors. There are tensors that hold actual data, containing a multi-dimensional array of numbers. On the other hand, there are tensors that only represent the result of a computation between one or more other tensors, and do not hold data until actually computed. We will explore this distinction soon.

Basic structure of a tensor

In ggml tensors are represented by the ggml_tensor struct. Simplified slightly for our purposes, it looks like the following:

// ggml.h
struct ggml_tensor {
    enum ggml_type    type;
    enum ggml_backend backend;

    int     n_dims;
    // number of elements
    int64_t ne[GGML_MAX_DIMS];
    // stride in bytes
    size_t  nb[GGML_MAX_DIMS];

    enum ggml_op op;

    struct ggml_tensor * src[GGML_MAX_SRC];

    void * data;

    char name[GGML_MAX_NAME];
};

The first few fields are straightforward:

• type contains the primitive type of the tensor’s elements. For example, GGML_TYPE_F32 means that each element is a 32-bit floating point number.
• enum contains whether the tensor is CPU-backed or GPU-backed. We’ll come back to this bit later.
• n_dims is the number of dimensions, which may range from 1 to 4.
• ne contains the number of elements in each dimension. ggml is row-major order, meaning that ne[0] marks the size of each row, ne[1] of each column and so on.

nb is a bit more sophisticated. It contains the stride: the number of bytes between consequetive elements in each dimension. In the first dimension this will be the size of the primitive element. In the second dimension it will be the row size times the size of an element, and so on. For example, for a 4x3x2 tensor:

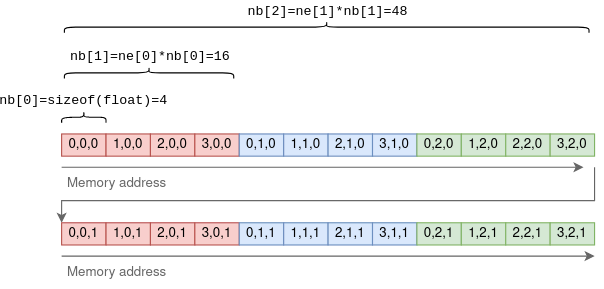
The purpose of using a stride is to allow certain tensor operations to be performed without copying any data. For example, the transpose operation on a two-dimensional that turns rows into columns can be carried out by just flipping ne and nb and pointing to the same underlying data:

// ggml.c (the function was slightly simplified).
struct ggml_tensor * ggml_transpose(
        struct ggml_context * ctx,
        struct ggml_tensor  * a) {
    // Initialize `result` to point to the same data as `a`
    struct ggml_tensor * result = ggml_view_tensor(ctx, a);

    result->ne[0] = a->ne[1];
    result->ne[1] = a->ne[0];

    result->nb[0] = a->nb[1];
    result->nb[1] = a->nb[0];

    result->op   = GGML_OP_TRANSPOSE;
    result->src[0] = a;

    return result;
}

In the above function, result is a new tensor initialized to point to the same multi-dimensional array of numbers as the source tensor a. By exchanging the dimensions in ne and the strides in nb, it performs the transpose operation without copying any data.

Tensor operations and views

As mentioned before, some tensors hold data, while others represent the theoretical result of an operation between other tensors. Going back to struct ggml_tensor:

• op may be any supported operation between tensors. Setting it to GGML_OP_NONE marks that the tensor holds data. Other values can mark an operation. For example, GGML_OP_MUL_MAT means that this tensor does not hold data, but only represents the result of matrix multiplication between two other tensors.
• src is an array of pointers to the tensors between which the operation is to be taken. For example, if op == GGML_OP_MUL_MAT, then src will contain pointers to the two tensors to be multiplied. If op == GGML_OP_NONE, then src will be empty.
• data points to the actual tensor’s data, or NULL if this tensor is an operation. It may also point to another tensor’s data, and then it’s known as a view. For example, in the ggml_transpose() function above, the resulting tensor is a view of the original, just with flipped dimensions and strides. data points to the same location in memory.

The matrix multiplication function illustrates these concepts well:

// ggml.c (simplified and commented)
struct ggml_tensor * ggml_mul_mat(
        struct ggml_context * ctx,
        struct ggml_tensor  * a,
        struct ggml_tensor  * b) {
    // Check that the tensors' dimensions permit matrix multiplication.
    GGML_ASSERT(ggml_can_mul_mat(a, b));

    // Set the new tensor's dimensions
    // according to matrix multiplication rules.
    const int64_t ne[4] = { a->ne[1], b->ne[1], b->ne[2], b->ne[3] };
    // Allocate a new ggml_tensor.
    // No data is actually allocated except the wrapper struct.
    struct ggml_tensor * result = ggml_new_tensor(ctx, GGML_TYPE_F32, MAX(a->n_dims, b->n_dims), ne);

    // Set the operation and sources.
    result->op   = GGML_OP_MUL_MAT;
    result->src[0] = a;
    result->src[1] = b;

    return result;
}

In the above function, result does not contain any data. It is merely a representation of the theoretical result of multiplying a and b.

Computing tensors

The ggml_mul_mat() function above, or any other tensor operation, does not calculate anything but just prepares the tensors for the operation. A different way to look at it is that it builds up a computation graph where each tensor operation is a node, and the operation’s sources are the node’s children. In the matrix multiplication scenario, the graph has a parent node with operation GGML_OP_MUL_MAT, along with two children.

As a real example from llama.cpp, the following code implements the self-attention mechanism which is part of each Transformer layer and will be explored more in-depth later:

// llama.cpp
static struct ggml_cgraph * llm_build_llama(/* ... */) {
    // ...

    // K,Q,V are tensors initialized earlier
    struct ggml_tensor * KQ = ggml_mul_mat(ctx0, K, Q);
    // KQ_scale is a single-number tensor initialized earlier.
    struct ggml_tensor * KQ_scaled = ggml_scale_inplace(ctx0, KQ, KQ_scale);
    struct ggml_tensor * KQ_masked = ggml_diag_mask_inf_inplace(ctx0, KQ_scaled, n_past);
    struct ggml_tensor * KQ_soft_max = ggml_soft_max_inplace(ctx0, KQ_masked);
    struct ggml_tensor * KQV = ggml_mul_mat(ctx0, V, KQ_soft_max);

    // ...
}

The code is a series of tensor operations and builds a computation graph that is identical to the one described in the original Transformer paper:

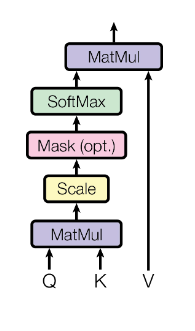
In order to actually compute the result tensor (here it’s KQV) the following steps are taken:

1. Data is loaded into each leaf tensor’s data pointer. In the example the leaf tensors are K, Q and V.
2. The output tensor (KQV) is converted to a computation graph using ggml_build_forward(). This function is relatively straightforward and orders the nodes in a depth-first order.¹
3. The computation graph is run using ggml_graph_compute(), which runs ggml_compute_forward() on each node in a depth-first order. ggml_compute_forward() does the heavy lifting of calculations. It performs the mathetmatical operation and fills the tensor’s data pointer with the result.
4. At the end of this process, the output tensor’s data pointer points to the final result.

Offloading calculations to the GPU

Many tensor operations like matrix addition and multiplication can be calculated on a GPU much more efficiently due to its high parallelism. When a GPU is available, tensors can be marked with tensor->backend = GGML_BACKEND_GPU. In this case, ggml_compute_forward() will attempt to offload the calculation to the GPU. The GPU will perform the tensor operation, and the result will be stored on the GPU’s memory (and not in the data pointer).

Consider the self-attention omputation graph shown before. Assuming that K,Q,V are fixed tensors, the computation can be offloaded to the GPU:

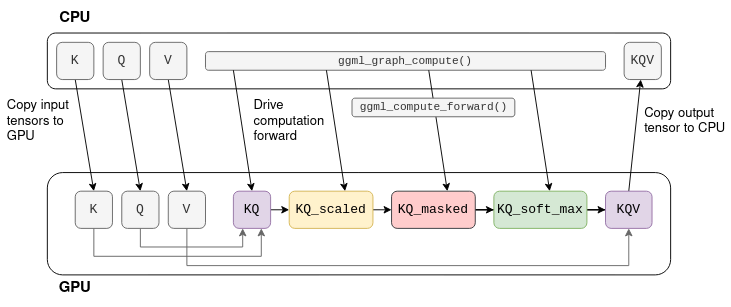
The process begins by copying K,Q,V to the GPU memory. The CPU then drives the computation forward tensor-by-tensor, but the actual mathematical operation is offloaded to the GPU. When the last operation in the graph ends, the result tensor’s data is copied back from the GPU memory to the CPU memory.

Note: In a real transformer K,Q,V are not fixed and KQV is not the final output. More on that later.

With this understanding of tensors, we can go back to the flow of LLaMA.

Tokenization

The first step in inference is tokenization. Tokenization is the process of splitting the prompt into a list of shorter strings known as tokens. The tokens must be part of the model’s vocabulary, which is the list of tokens the LLM was trained on. LLaMA’s vocabulary, for example, consists of 32k tokens and is distributed as part of the model.

For our example prompt, the tokenization splits the prompt into eleven tokens (spaces are replaced with the special meta symbol ’▁’ (U+2581)):

|Quant|um|▁mechan|ics|▁is|▁a|▁fundamental|▁theory|▁in|▁physics|▁that|

For tokenization, LLaMA uses the SentencePiece tokenizer with the byte-pair-encoding (BPE) algorithm. This tokenizer is interesting because it is subword-based, meaning that words may be represented by multiple tokens. In our prompt, for example, ‘Quantum’ is split into ‘Quant’ and ‘um’. During training, when the vocabulary is derived, the BPE algorithm ensures that common words are included in the vocabulary as a single token, while rare words are broken down into subwords. In the example above, the word ‘Quantum’ is not part of the vocabulary, but ‘Quant’ and ‘um’ are as two separate tokens. White spaces are not treated specially, and are included in the tokens themselves as the meta character if they are common enough.

Subword-based tokenization is powerful due to multiple reasons:

• It allows the LLM to learn the meaning of rare words like ‘Quantum’ while keeping the vocabulary size relatively small by representing common suffixes and prefixes as separate tokens.
• It learns language-specific features without employing language-specific tokenization schemes. Quoting from the BPE-encoding paper:

  consider compounds such as the German Abwasser|behandlungs|anlange ‘sewage water treatment plant’, for which a segmented, variable-length representation is intuitively more appealing than encoding the word as a fixed-length vector.

• Similarly, it is also useful in parsing code. For example, a variable named model_size will be tokenized into model|_|size, allowing the LLM to “understand” the purpose of the variable (yet another reason to give your variables indicative names!).

In llama.cpp, tokenization is performed using the llama_tokenize() function. This function takes the prompt string as input and returns a list of tokens, where each token is represented by an integer:

// llama.h
typedef int llama_token;

// common.h
std::vector<llama_token> llama_tokenize(
        struct llama_context * ctx,
        // the prompt
        const std::string & text,
        bool   add_bos);

The tokenization process starts by breaking down the prompt into single-character tokens. Then, it iteratively tries to merge each two consequetive tokens into a larger one, as long as the merged token is part of the vocabulary. This ensures that the resulting tokens are as large as possible. For our example prompt, the tokenization steps are as follows:

Q|u|a|n|t|u|m|▁|m|e|c|h|a|n|i|c|s|▁|i|s|▁a|▁|f|u|n|d|a|m|e|n|t|a|l|

Qu|an|t|um|▁m|e|ch|an|ic|s|▁|is|▁a|▁f|u|nd|am|en|t|al|

Qu|ant|um|▁me|chan|ics|▁is|▁a|▁f|und|am|ent|al|

Quant|um|▁mechan|ics|▁is|▁a|▁fund|ament|al|

Quant|um|▁mechan|ics|▁is|▁a|▁fund|amental|

Quant|um|▁mechan|ics|▁is|▁a|▁fundamental|

Note that each intermediate step consists of valid tokenization according to the model’s vocabulary. However, only the last one is used as the input to the LLM.

Embeddings

The tokens are used as input to LLaMA to predict the next token. The key function here is the llm_build_llama() function:

// llama.cpp (simplified)
static struct ggml_cgraph * llm_build_llama(
         llama_context & lctx,
     const llama_token * tokens,
                   int   n_tokens,
                   int   n_past);

This function takes a list of tokens represented by the tokens and n_tokens parameters as input. It then builds the full tensor computation graph of LLaMA, and returns it as a struct ggml_cgraph. No computation actually takes place at this stage. The n_past parameter, which is currently set to zero, can be ignored for now. We will revisit it later when discussing the kv cache.

Beside the tokens, the function makes use of the model weights, or model parameters. These are fixed tensors learned during the LLM training process and included as part of the model. These model parameters are pre-loaded into lctx before the inference begins.

We will now begin exploring the computation graph structure. The first part of this computation graph involves converting the tokens into embeddings.

An embedding is a fixed vector representation of each token that is more suitable for deep learning than pure integers, as it captures the semantic meaning of words. The size of this vector is the model dimension, which varies between models. In LLaMA-7B, for example, the model dimension is n_embd=4096.

The model parameters include a token-embedding matrix that converts tokens into embeddings. Since our vocabulary size is n_vocab=32000, this is a 32000 x 4096 matrix with each row containing the embedding vector for one token:

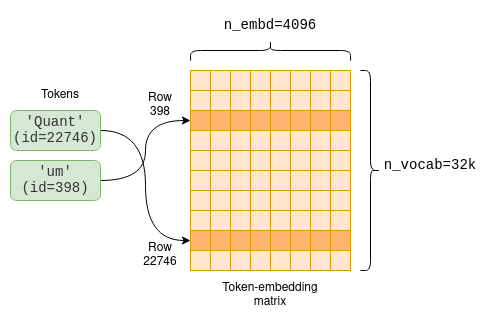
The first part of the computation graph extracts the relevant rows from the token-embedding matrix for each token:

// llama.cpp (simplified)
static struct ggml_cgraph * llm_build_llama(/* ... */) {
    // ...

    struct ggml_tensor * inp_tokens = ggml_new_tensor_1d(ctx0, GGML_TYPE_I32, n_tokens);
    memcpy(
        inp_tokens->data,
        tokens,
        n_tokens * ggml_element_size(inp_tokens));

    inpL = ggml_get_rows(ctx0, model.tok_embeddings, inp_tokens);
}
//

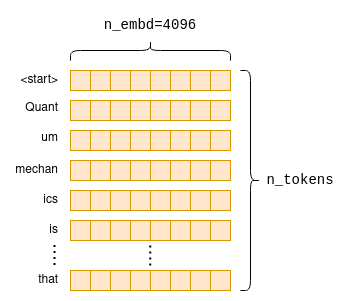
The code first creates a new one-dimensional tensor of integers, called inp_tokens, to hold the numerical tokens. Then, it copies the token values into this tensor’s data pointer. Last, it creates a new GGML_OP_GET_ROWS tensor operation combining the token-embedding matrix model.tok_embeddings with our tokens.

This operation, when later computed, pulls rows from the embeddings matrix as shown in the diagram above to create a new n_tokens x n_embd matrix containing only the embeddings for our tokens in their original order:

The Transformer

The main part of the computation graph is called the Transformer. The Transformer is a neural network architecture that is the core of the LLM, and performs the main inference logic. In the following section we will explore some key aspects of the transformer from an engineering perspective, focusing on the self-attention mechanism. If you want to gain an understanding of the intuition behind the Transformer’s architecture instead, I recommend reading The Illustrated Transformer².

Self-attention

We first zoom in to look at what self-attention is; after which we will zoom back out to see how it fits within the overall Transformer architecture³.

Self-attention is a mechanism that takes a sequence of tokens and produces a compact vector representation of that sequence, taking into account the relationships between the tokens. It is the only place within the LLM architecture where the relationships between the tokens are computed. Therefore, it forms the core of language comprehension, which entails understanding word relationships. Since it involves cross-token computations, it is also the most interesting place from an engineering perspective, as the computations can grow quite large, especially for longer sequences.

The input to the self-attention mechanism is the n_tokens x n_embd embedding matrix, with each row, or vector, representing an indivisual token⁴. Each of these vectors is then transformed into three distinct vectors, called “key”, “query” and “value” vectors. The transformation is achieved by multiplying the embedding vector of each token with the fixed wk, wq and wv matrices, which are part of the model parameters:

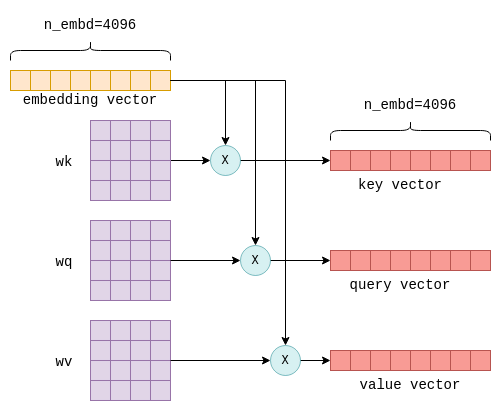
This process is repeated for every token, i.e. n_tokens times. Theoretically, this could be done in a loop but for efficiency all rows are transformed in a single operation using matrix multiplication, which does exactly that. The relevant code looks as follows:

// llama.cpp (simplified to remove use of cache)

// `cur` contains the input to the self-attention mechanism
struct ggml_tensor * K = ggml_mul_mat(ctx0,
    model.layers[il].wk, cur);
struct ggml_tensor * Q = ggml_mul_mat(ctx0,
    model.layers[il].wq, cur);
struct ggml_tensor * V = ggml_mul_mat(ctx0,
    model.layers[il].wv, cur);

We end up with K,Q and V: Three matrices, also of size n_tokens x n_embd, with the key, query and value vectors for each token stacked together.

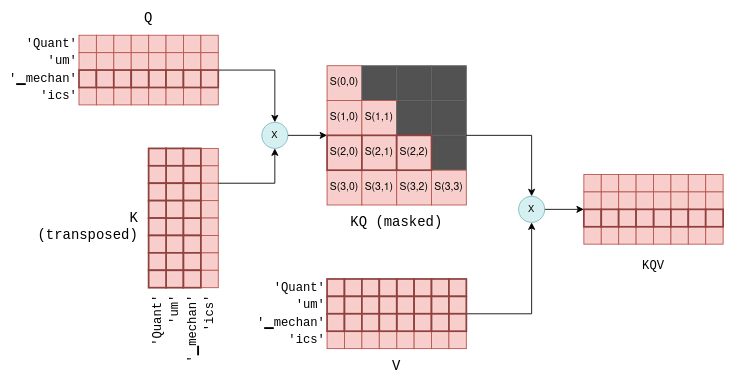
The next step of self-attention involves multiplying the matrix Q, which contains the stacked query vectors, with the transpose of the matrix K, which contains the stacked key vectors. For those less familiar with matrix operations, this operation essentially calculates a joint score for each pair of query and key vectors. We will use the notation S(i,j) to denote the score of query i with key j.

This process yield n_tokens^2 scores, one for each query-key pair, packed within a single matrix called KQ. This matrix is subsequently masked to remove the entries above the diagonal:

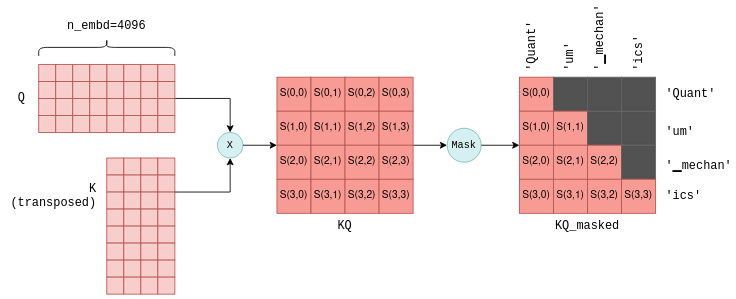
The masking operation is a critical step. For each token it retains scores only with its preceeding tokens. During the training phase, this constraint ensures that the LLM learns to predict tokens based solely on past tokens, rather than future ones. Moreover, as we’ll explore in more detail later, it allows for significant optimizations when predicting future tokens.

The last step of self-attention involves multiplying the masked scoring KQ_masked with the value vectors from before⁵. Such a matrix multiplication operation creates a weighted sum of the value vectors of all preceeding tokens, where the weights are the scores S(i,j). For example, for the fourth token ics it creates a weighted sum of the value vectors of Quant, um, ▁mechan and ics with the weights S(3,0) to S(3,3), which themselves were calculated from the query vector of ics and all preceeding key vectors.

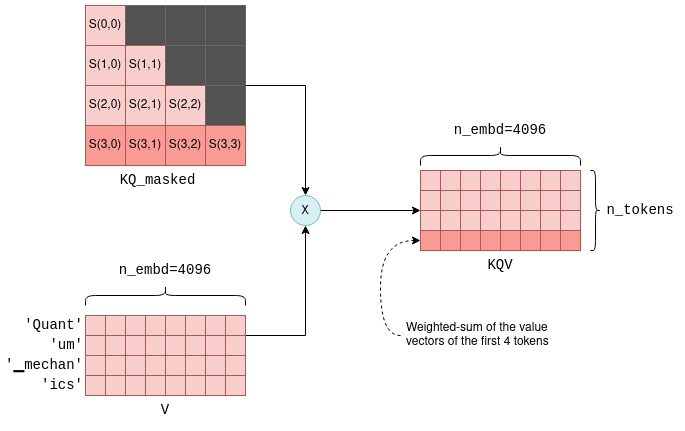
The KQV matrix concludes the self-attention mechanism. The relevant code implementing self-attention was already presented before in the context of general tensor computations, but now you are better equipped fully understand it.

The layers of the Transformer

Self-attention is one of the components in what are called the layers of the transformer. Each layer, in addition to the self-attention mechanism, contains multiple other tensor operations, mostly matrix addition, multiplication and activation that are part of a feed-forward neural network. We will not explore these more in detail, but just note the following facts:

• Large, fixed, parameter matrices are used in the feed-forward network. In LLaMA-7B, their sizes are n_embd x n_ff = 4096 x 11008.
• Besides self-attention, all other operations can be thought of as being carried row-by-row, or token-by-token. As mentioned before, only self-attention contains cross-token calculations. This will be important later when discussing the kv-cache.
• The input and output are always of size n_tokens x n_embd: One row for each token, each the size of the model’s dimension.

For completeness I included a diagram of a single Transformer layer in LLaMA-7B. Note that the exact architecture will most likely vary slightly in future models.

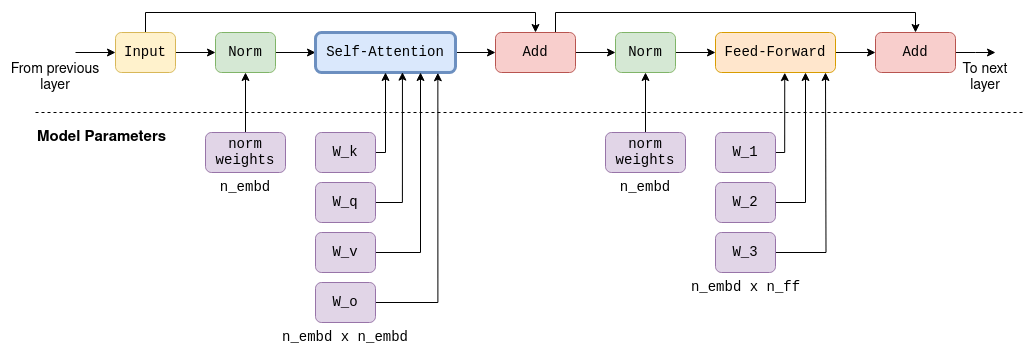
In a Transformer architecture there are multiple layers. For example, in LLaMA-7B there are n_layers=32 layers. The layers are identical except that each has its own set of parameter matrices (e.g. its own wk, wq and wv matrices for the self-attention mechanism). The first layer’s input is the embedding matrix as described above. The first layer’s output is then used as the input to the second layer and so on. We can think of it as if each layer produces a list of embeddings, but each embedding no longer tied directly to a single token but rather to some kind of more complex understanding of token relationships.

Calculating the logits

The final step of the Transformer involves the computation of logits. A logit is a floating-point number that represents the probability that a particular token is the “correct” next token. The higher the value of the logit, the more likely it is that the corresponding token is the “correct” one.

The logits are calculated by multiplying the output of the last Transformer layer with a fixed n_embd x n_vocab parameter matrix (also called output in llama.cpp). This operation results in a logit for each token in our vocabulary. For example, in LLaMA, it results in n_vocab=32000 logits:

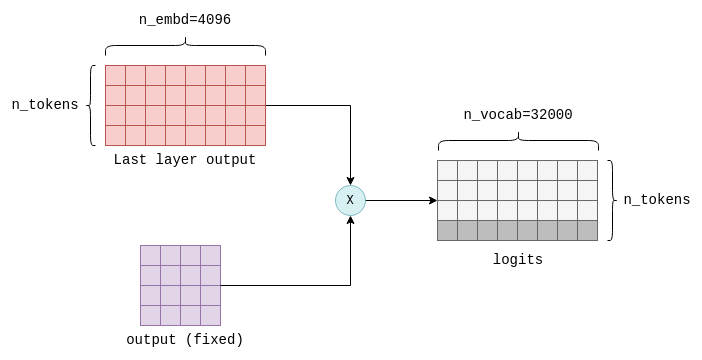
The logits are the Transformer’s output and tell us what the most likely next tokens are. By this all the tensor computations are concluded. The following simplified and commented version of the llm_build_llama() function summarizes all steps which were described in this section:

// llama.cpp (simplified and commented)

static struct ggml_cgraph * llm_build_llama(
         llama_context & lctx,
     const llama_token * tokens,
                   int   n_tokens,
                   int   n_past) {
    ggml_cgraph * gf = ggml_new_graph(ctx0);
    struct ggml_tensor * cur;
    struct ggml_tensor * inpL;

    // Create a tensor to hold the tokens.
    struct ggml_tensor * inp_tokens = ggml_new_tensor_1d(ctx0, GGML_TYPE_I32, N);
    // Copy the tokens into the tensor
    memcpy(
        inp_tokens->data,
        tokens,
        n_tokens * ggml_element_size(inp_tokens));

    // Create the embedding matrix.
    inpL = ggml_get_rows(ctx0,
        model.tok_embeddings,
        inp_tokens);

    // Iteratively apply all layers.
    for (int il = 0; il < n_layer; ++il) {
        struct ggml_tensor * K = ggml_mul_mat(ctx0, model.layers[il].wk, cur);
        struct ggml_tensor * Q = ggml_mul_mat(ctx0, model.layers[il].wq, cur);
        struct ggml_tensor * V = ggml_mul_mat(ctx0, model.layers[il].wv, cur);

        struct ggml_tensor * KQ = ggml_mul_mat(ctx0, K, Q);
        struct ggml_tensor * KQ_scaled = ggml_scale_inplace(ctx0, KQ, KQ_scale);
        struct ggml_tensor * KQ_masked = ggml_diag_mask_inf_inplace(ctx0,
            KQ_scaled, n_past);
        struct ggml_tensor * KQ_soft_max = ggml_soft_max_inplace(ctx0, KQ_masked);
        struct ggml_tensor * KQV = ggml_mul_mat(ctx0, V, KQ_soft_max);

        // Run feed-forward network.
        // Produces `cur`.
        // ...

        // input for next layer
        inpL = cur;
    }

    cur = inpL;

    // Calculate logits from last layer's output.
    cur = ggml_mul_mat(ctx0, model.output, cur);

    // Build and return the computation graph.
    ggml_build_forward_expand(gf, cur);
    return gf;
}

To actually performn inference, the computation graph returned by this function is computed, using ggml_graph_compute() as described previously. The logits are then copied out from the last tensor’s data pointer into an array of floats, ready for the next step called sampling.

Sampling

With the list of logits in hand, the next step is to choose the next token based on them. This process is called sampling. There are multiple sampling methods available, suitable for different use cases. In this section we will cover two basic sampling methods, with more advanced sampling methods like grammar sampling reserved for future posts.

Greedy sampling

Greedy sampling is a straightforward approach that selects the token with the highest logit associated with it.

For our example prompt, the following tokens have the highest logits:

Therefore, greedy sampling will deterministically choose ▁describes as the next token. Greedy sampling is most useful when deterministic outputs are required when re-evaluating identical prompts.

Temperature sampling

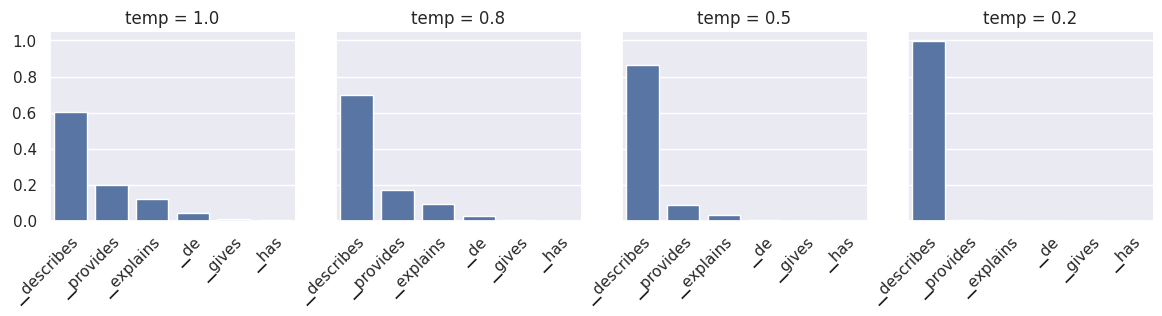
Temperature sampling is probabilistic, meaning that the same prompt might produce different outputs when re-evaluated. It uses a parameter called temperature which is a floating-point value between 0 and 1 and affects the randomness of the result. The process goes as follows:

1. The logits are sorted from high to low and normalized using a softmax function to ensure that they all sum to 1. This transformation converts each logit into a probability.
2. A threshold (set to 0.95 by default) is applied, retaining only the top tokens such that their cumulative probability remains below the threshold. This step effectively removes low-probability tokens, preventing “bad” or “incorrect” tokens from being rarely sampled.
3. The remaining logits are divided by the temperature parameter and normalized again such that they all sum to 1 and represent probabilities.
4. A token is randomly sampled based on these probabilities. For example, in our prompt, the token ▁describes has a probability of p=0.6, meaning that it will be chosen approximately 60% of the time. Upon re-evaluation, different tokens may be chosen.

The temperature parameter in step 3 serves to either increase or decrease randomness. Lower temperature values suppress lower probability tokens, making it more likely that the same tokens will be chosen on re-evaluation. Therefore, lower temperature values decrease randomness. In contrast, higher temperature values tend to “flatten” the probability distribution, emphasizing lower probability tokens. This increases the likelihood that each re-evaluation will result in different tokens, increasing randomness.

Sampling a token concludes a full iteration of the LLM. After the initial token is sampled, it is added to the list of tokens, and the entire process runs again. The output iteratively becomes the input to the LLM, increasing by one token each iteration.

Theoretically, subsequent iterations can be carried out identically. However, to address performance degradation as the list of tokens grows, certain optimizations are employed. These will be covered next.

Optimizing inference

The self-attention stage of the Transformer can become a performance bottleneck as the list of input tokens to the LLM grows. A longer list of tokens means that larger matrices are multiplied together. Each matrix multiplication consists of many smaller numerical operations, known as floating-point operations, which are constrained by the GPU’s floating-point-operations-per-second capacity (flops). In the Transformer Inference Arithmetic, it is calculated that for a 52B parameter model, on an A100 GPU, performance starts to degrade at 208 tokens due to excessive flops. The most commonly employed optimization technique to solve this bottleneck is known as the kv cache.

The KV cache

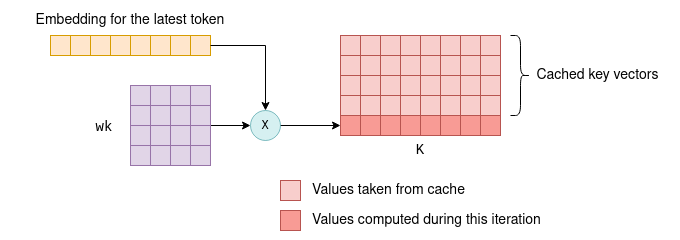
To recap, each token has an associated embedding vector, which is further transformed into key and value vectors by multiplying it with the parameter matrices wk and wv. The kv cache is a cache for these key and value vectors. By caching them, we save the floating point operations required for re-calculating them on each iteration.

The cache works as follows:

• During the initial iteration, the key and value vectors are computed for all tokens, as previously described, and then saved into the kv cache.
• In subsequent iterations, only the key and value vectors for the newest token need to be calculated. The cached k-v vectors, together with the k-v vectors for the new token, are concatenated together to form the K and V matrices. This saves recalculating the k-v vectors for all previous tokens, which can be significant.

The ability to utilize a cache for key and value vectors arises from the fact that these vectors remain identical between iterations. For example, if we first process four tokens, and then five tokens, with the initial four unchanged, then the first four key and value vectors will remain identical between the first and the second iteration. As a result, there’s no need to recalculate key and value vectors for the first four tokens in the second iteration.

This principle holds true for all layers within the Transformer, not just the first one. In all layers, the key and value vectors for each token are solely dependent on previous tokens. Therefore, as new tokens are appended in subsequent iterations, the key and value vectors for existing tokens remain the same.

For the first layer, this concept is relatively straightforward to verify: the key vector of a token is determined by multiplying the token’s fixed embedding with the fixed wk parameter matrix. Thus, it remains unchanged in subsequent iterations, regardless of the additional tokens introduced. The same rationale applies to the value vector.

For the second layer and beyond, this principle is a bit less obvious but still holds true. To understand why, consider the first layer’s KQV matrix, the output of the self-attention stage. Each row in the KQV matrix is a weighted sum that depends on:

• Value vectors of previous tokens.
• Scores calculated from key vectors of previous tokens.

Therefore each row in KQV solely relies on previous tokens. This matrix, following a few additional row-based operations, serves as the input to the second layer. This implies that the second layer’s input will remain unchanged in future iterations, except for the addition of new rows. Inductively, the same logic extends to the rest of the layers.

Further optimizing subsequent iterations

You might wonder why we don’t cache the query vectors as well, considering we cache the key and value vectors. The answer is that in fact, except for the query vector of the current token, query vectors for previous tokens are unnecessary in subsequent iterations. With the kv cache in place, we can actually feed the self-attention mechanism only with the latest token’s query vector. This query vector is multiplied with the cached K matrix to calculate the joint scores of the last token and all previous tokens. Then, it is multiplied with the cached V matrix to calculate only the latest row of the KQV matrix. In fact, across all layers, we now pass 1 x n_embd -sized vectors instead of the n_token x n_embd matrices calculated in the first iteration. To illustrate this, compare the following diagram, showing a later iteration, with the previous one:

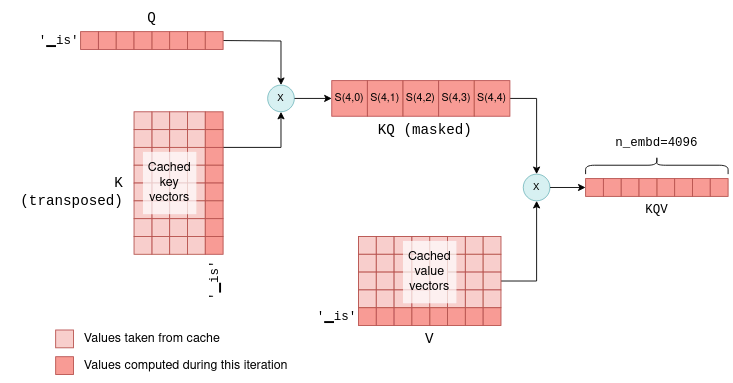
This process repeats across all layers, utilizing each layer’s kv cache. As a result, the Transformer’s output in this case is a single vector of n_vocab logits predicting the next token.

With this optimization we save floating point operations of calculating unnecessary rows in KQ and KQV, which can become quite significant as the list of tokens grows in size.

The KV cache in practice

We can dive into llama.cpp code to see how the kv cache is implemented in practice. Unsurprisingly maybe, it is built using tensors, one for key vectors and one for value vectors:

// llama.cpp (simplified)

struct llama_kv_cache {
    // cache of key vectors
    struct ggml_tensor * k = NULL;

    // cache of value vectors
    struct ggml_tensor * v = NULL;

    int n; // number of tokens currently in the cache
};

When the cache is initialized, enough space is allocated to hold 512 key and value vectors for each layer:

// llama.cpp (simplified)
// n_ctx = 512 by default
static bool llama_kv_cache_init(
    struct llama_kv_cache & cache,
    ggml_type   wtype,
    int   n_ctx) {
    // Allocate enough elements to hold n_ctx vectors for each layer.
    const int64_t n_elements = n_embd*n_layer*n_ctx;

    cache.k = ggml_new_tensor_1d(cache.ctx, wtype, n_elements);
    cache.v = ggml_new_tensor_1d(cache.ctx, wtype, n_elements);

    // ...
}

Recall that during inference, the computation graph is built using the function llm_build_llama(). This function has a parameter called n_past that we ignored before. In the first iteration, the n_tokens parameter contains the number of tokens and n_past is set to 0. In subsequent iterations, n_tokens is set to 1 because only the latest token is processed, and n_past contains the number of past tokens. n_past is then used to pull the correct number of key and value vectors from the kv cache.

The relevant part from this function is shown here, utilizing the cache for calculating the K matrix. I simplified it slightly to ignore the multi-head attention and added comments for each step:

// llama.cpp (simplified and commented)

static struct ggml_cgraph * llm_build_llama(
    llama_context & lctx,
    const llama_token * tokens,
    int   n_tokens,
    int   n_past) {
    // ...

    // Iteratively apply all layers.
    for (int il = 0; il < n_layer; ++il) {
         // Compute the key vector of the latest token.
         struct ggml_tensor * Kcur = ggml_mul_mat(ctx0, model.layers[il].wk, cur);
         // Build a view of size n_embd into an empty slot in the cache.
         struct ggml_tensor * k = ggml_view_1d(
            ctx0,
            kv_cache.k,
            // size
            n_tokens*n_embd,
            // offset
            (ggml_element_size(kv_cache.k)*n_embd) * (il*n_ctx + n_past)
         );

         // Copy latest token's k vector into the empty cache slot.
         ggml_cpy(ctx0, Kcur, k);

         // Form the K matrix by taking a view of the cache.
         struct ggml_tensor * K =
             ggml_view_2d(ctx0,
                 kv_self.k,
                 // row size
                 n_embd,
                 // number of rows
                 n_past + n_tokens,
                 // stride
                 ggml_element_size(kv_self.k) * n_embd,
                 // cache offset
                 ggml_element_size(kv_self.k) * n_embd * n_ctx * il);
    }
}

First, the new key vector is calculated. Then, n_past is used to find the next empty slot in the cache, and the new key vector is copied there. Last, the matrix K is formed by taking a view into the cache with the correct number of tokens (n_past + n_tokens).

The kv cache is the basis for LLM inference optimization. It’s worth noting that the version implemented in llama.cpp (as of this writing) and presented here is not the most optimal one. For instance, it allocates a lot of memory in advance to hold the maximum number of key and value vectors supported (512 in this case). More advanced implementations, such as vLLM, aim to enhance memory usage efficiency and may offer further performance improvement. These advanced techniques are reserved for future posts. Moreover, as this field moves forward at lightning speeds, there are likely to be new and improved optimization techniques in the future.

Concluding

This post covered quite a lot of ground and should give you a basic understanding of the full process of LLM inference. With this knowledge you can get around more advanced resources:

• LLM parameter counting and Transformer Inference Arithmetic analyze LLM performance in depth.
• vLLM is a library for managing the kv cache memory more efficiently.
• Continuous batching is an optimization technique to batch multiple LLM prompts together.

I also hope to cover the internals of more advanced topics in future posts. Some options include:

• Quantized models.
• Fine-tuned LLMs using LoRA.
• Various attention mechanisms (Multi-head attention, Grouped-query attention and Sliding window attention).
• LLM request batching.
• Grammar sampling.

Stay tuned!

Footnotes